The true risk of stocks for the long run (part 1)

Are retail investors taking more risk than they realize? The following discussion is directed towards individual investors who are saving for long term goals such as retirement, primarily using a buy-and-hold approach in accounts like a 401k. The conventional wisdom says that the more time until you need your principal, the more risk you can afford to take, and therefore you should invest more in stocks. What is the logic behind this? Let’s say someone offers you a $100 “investment” based on a coin flip. Heads, you earn 33%, tails, you lose 25%. So after one flip you’ll either have $133 or $75. Since each outcome is equally likely (50/50), on average your $100 investment will return $104, or 4%. That’s not too bad. Let’s imagine that each coin-flip in this example is equal to one year of investing in the stock market. Here’s what a simple payoff tree looks like:


However, you can make this investment multiple times. Every time you flip the coin, there is still a 50/50 chance of heads/tails, and the payoffs remain the same. Since the coin is random, you figure that the more times you flip it, the more likely it is that the total number of heads versus tails will even out. This is equivalent to investing over multiple years. Your financial adviser confirms your intuition and tells you that historically, the variation of stock market returns decreases as you invest over longer period of times. It’s a reasonable-sounding (but flawed) assumption that the more times you flip, the less likely you are to get a bunch of heads or tails in a row. But you believe what your financial adviser tells you, so you expect the risk of this investment to go down if you’re willing to flip it four times instead of just once. Here’s what the payoff tree looks like now:


The average ending portfolio value (probability weighted average) is now $117, which is your 4% expected return compounded 4 times. However, something strange has happened with the ending values. The dispersion between the best and worst cases has increased, from $313 to $31. You also notice that there’s a 70% chance (6% + 25% + 38%) you don’t do any better than break even, and a 31% chance (6% + 25%) that your $100 investment is worth $56 or less after 4 flips. If this money was needed to support you in retirement, would you consider these to be good odds? Is your coin-flip investment (stocks) really better than a less risky alternative investment that might guarantee you an ending value of $106 over four years but with no downside risk? This graph from the Wall Street Journal shows that anyone who started investing after 1996 would’ve been better off in a no-risk money market account than in a broad market index:


Consider the coin flip investment similar to investing in stocks. As you increase the number of investment periods above 4, the trends illustrated in this overly simplified example only continue to increase. The best case gets much better, and the worst case gets much worse. The risk of a substantial shortfall increases as you flip the coin more times. This is contrary to the traditional wisdom that a longer investment horizon reduces the risk of volatile assets. I’ve written about the myth of time diversification before, but this example clearly illustrates how the risk to your portfolio’s final value increases, rather than decreases, over time. At the end of the day, the final value is what matters – standard deviation and expected returns are great, but you can’t eat them.

My point is not that investors should avoid stocks entirely, but that they should be aware of the fact that investing for the long term does not eliminate the risk of stocks. Riskier assets have a higher expected return, but not necessarily a higher realized return. You are not guaranteed a higher return just because you took more risk. If investors are going to be compensated for taking risk, then there has to be a real risk of loss over the long term or else why would the risk premium exist? If you still don’t believe me, take a look at a graph of the Nikkei over the last 25 years:


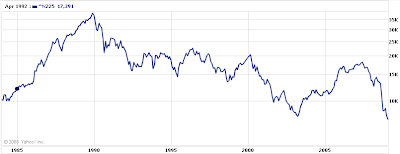
If you think I’m being overly pessimistic, or if you think the Japanese economy is sufficiently different from the US economy, then how about the returns on the S&P 500 from 1966-1982?